Quadratic Equation Calculator

A Quadratic Equation Calculator is a powerful tool designed to solve quadratic equations quickly and accurately. Whether you’re a student, a professional, or someone brushing up on algebra, this calculator simplifies the process of finding solutions to second-degree polynomial equations. In this article, we’ll explore quadratic equations, how to use the calculator effectively, its underlying mechanics, features, and the importance of the discriminant in understanding solutions.

Results:

What is a Quadratic Equation?

A quadratic equation is a polynomial equation of degree 2, typically expressed in the standard form:

$$ax^2+bx+c=0$$

Here:

• a, b, and c are constants, with a≠0
• x is the variable.

The term “quadratic” comes from the Latin word quadratus, meaning square, as the variable x is squared. They have numerous real-world applications, including physics (e.g., projectile motion), engineering, and economics.

Real-World Applications

Quadratic equations are not just theoretical, they have numerous practical applications:

• Physics: Calculating projectile motion trajectories.
• Engineering: Designing parabolic structures like bridges or satellite dishes.
• Finance: Modeling profit maximization or cost minimization problems.
• Biology: Predicting population growth under certain conditions.

Roots 

The solutions are called its roots. These roots can be:

• Real and distinct (two solutions),
• Real and repeated (one solution),
• Complex (no real solution).

The roots are often found using the formula:

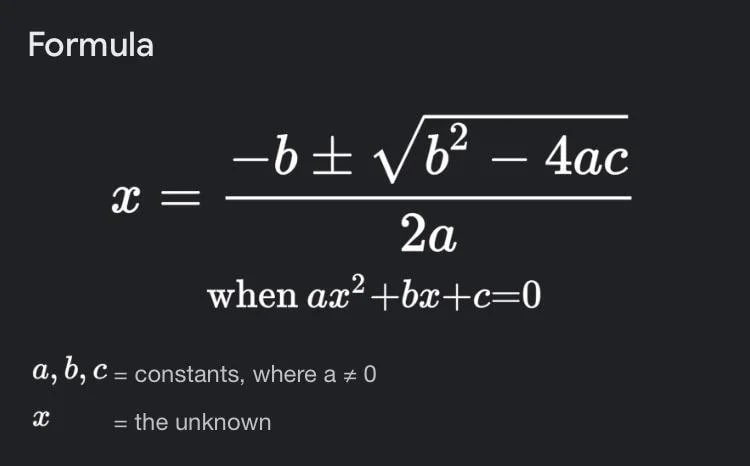
Understanding this formula is critical for solving equations manually or through a calculator.

Why Are These Equations Important?

They  are foundational in mathematics because they describe relationships involving squared terms, which appear frequently in nature and science. Their study builds essential problem-solving skills and helps understand more complex mathematical concepts like calculus and differential equations.

How to Use the Calculator

Using a quadratic equation calculator is straightforward. Follow these steps:

1. Input the coefficients: Enter the values of a, b, and c from your equation (ax2+bx+c=0).
2. Press calculate: The calculator processes the inputs using the quadratic formula.
3. View results: The calculator displays the roots, whether they are real or complex.

For example:

• For x2−3x−4=0
• a=1,b=−3,c=−4), the calculator will return two real roots: 
• x=4 and x=−1.

How Does the Calculator Work?

A quadratic equation calculator solves by using the formula:

$$x = {-b \pm \sqrt{b^2-4ac} \over 2a}$$

Key Steps:

1. Calculate the discriminant b2−4ac:

• Determines the nature of the roots.
• If $b^2−4ac>0$: Two distinct real roots.
• If $b^2−4ac=0$: One real repeated root.
• If $b^2−4ac<0$:Two complex roots.

2. Compute square root and divide:

• Determines the nature of the roots.
  • The calculator computes 
  • $b^2−4ac$ and applies it to find both solutions (+ and −).
• Output solutions:
  • Displays results in simplified form, including complex numbers if necessary.

Advanced calculators may also graphically represent solutions or provide step-by-step calculations for better understanding.

Features of the Calculator

Today’s calculators incorporate so many features for better user experience:

• Works with all types of radicands: Both real radical and all complex roots are displayed.
• Interactive operations: Showing intermediate answers for lessons is a feature on some calculators.
• Visually interactive: Illustrates the condition of a parabola relative to the x-axis, whether it intersects or does not touch.
• Error alerting: Notifies the user when invalid inputs are made or a=0 
• Calculative speed and precision: System can solve the algebraic equations by itself in a split second.

It follows that such calculators are extremely useful for students and for engineers dealing with algebraic equations among other professionals as well.

Understanding the Discriminant

The discriminant is a mathematical term that is very essential for the solution of any quadratic equation. Description: The discriminant is derived from the formula as follows:

$$D=b^2−4ac$$

This value appearing below the square root, also called structural, determines the resolve’s structure and quantity. It helps to analyze how the solution is going to behave or what sort of solutions one is going to get without solving it completely. Such characteristics make it more valuable in mathematics and other complexities.

Particularly for the discriminant it is important to know because it allows to study the graph of the equation. The roots are equal to the x – axes cut of the graph of the function which is parabolic. The discriminant makes it possible to analyze how this parabola is positioned with respect to the x-axis – whether it cuts it twice, one or not at all.

Discriminant (D)	Nature of Roots	Description
D>0	Two distinct real roots	The parabola crosses the x-axis twice.
D=0	One repeated real root	The parabola touches the x-axis once.
D<0	Two complex roots	The parabola does not intersect the x-axis.

For example:

1. For x2+4x+4=0
2. $D=b^2−4ac=(4)^2−(4)(1)(4)=0$ This yields one repeated root.
3. For $x^2+x+1=0$
4. $D=x^2−4ac=(1)^2−(4)(1)(1)=−3<0$ This results in two complex roots.

The discriminant not only aids in solving equations but also helps understand their graphical behavior.

Importance of Understanding Discriminants

Understanding discriminants is essential efficiently and interpreting their solutions correctly. It allows mathematicians and professionals to quickly determine whether has real or complex solutions and how these solutions relate to practical scenarios.

The discriminant not only determines the type of roots but also helps professionals and mathematicians understand how these roots relate to real-world problems. For example, in physics, a positive discriminant might indicate two possible times for an object to reach a certain height, while a negative discriminant might suggest that a solution is not feasible in real-world conditions.

Conclusion

A Quadratic Equation Calculator is an invaluable tool for solving second-degree polynomial equations efficiently and accurately. By leveraging mathematical algorithms like the formula, it eliminates manual errors and saves time for users across various fields—from students learning algebra to professionals tackling engineering problems.

Understanding concepts such as roots, discriminants, and how these calculators work enhances your ability to approach confidently. Whether you’re solving for real-world applications or academic purposes, this tool simplifies even complex problems into manageable solutions.

Frequently Asked Questions (FAQs)