Logarithmic Equation Calculator

In the realm of mathematics, logarithmic equations play a crucial role in various fields, from physics and chemistry to finance and computer science. These equations, often complex and time-consuming to solve manually, have become much more manageable with the advent of logarithmic equation calculators. These powerful tools have revolutionized the way we approach and solve logarithmic problems, offering speed, accuracy, and convenience.

As we delve into the world of logarithmic equation calculators, we’ll explore their features, usage, and the numerous benefits they bring to students, professionals, and researchers alike. Whether you’re grappling with basic concepts or tackling advanced equations, understanding and utilizing these calculators can significantly enhance your problem-solving capabilities.

What is a Logarithmic Equation?

A logarithmic equation is a mathematical expression that involves logarithms of variables or expressions. In its most basic form, a this equation can be expressed as:

$$log⁡b(x)=y$$

Where:

• b is the base of the logarithm
• x is the argument or the number whose logarithm is being calculated
• y is the exponent to which the base must be raised to obtain x

Logarithms are essentially the inverse operations of exponentiation. They answer the question: “To what power must we raise a certain number (the base) to obtain another number?”

Logarithmic equations can appear in various forms, from simple to complex. They often require applying specific properties of logarithms for simplification, such as:

• Product Rule: $log⁡b(xy)=log⁡b(x)+log⁡b(y)$
• Quotient Rule: $log⁡b(x/y)=log⁡b(x)−log⁡b(y)$
• Power Rule: $log⁡b(x^y)=ylog⁡b(x)$

Understanding these rules is crucial for solving equations efficiently.

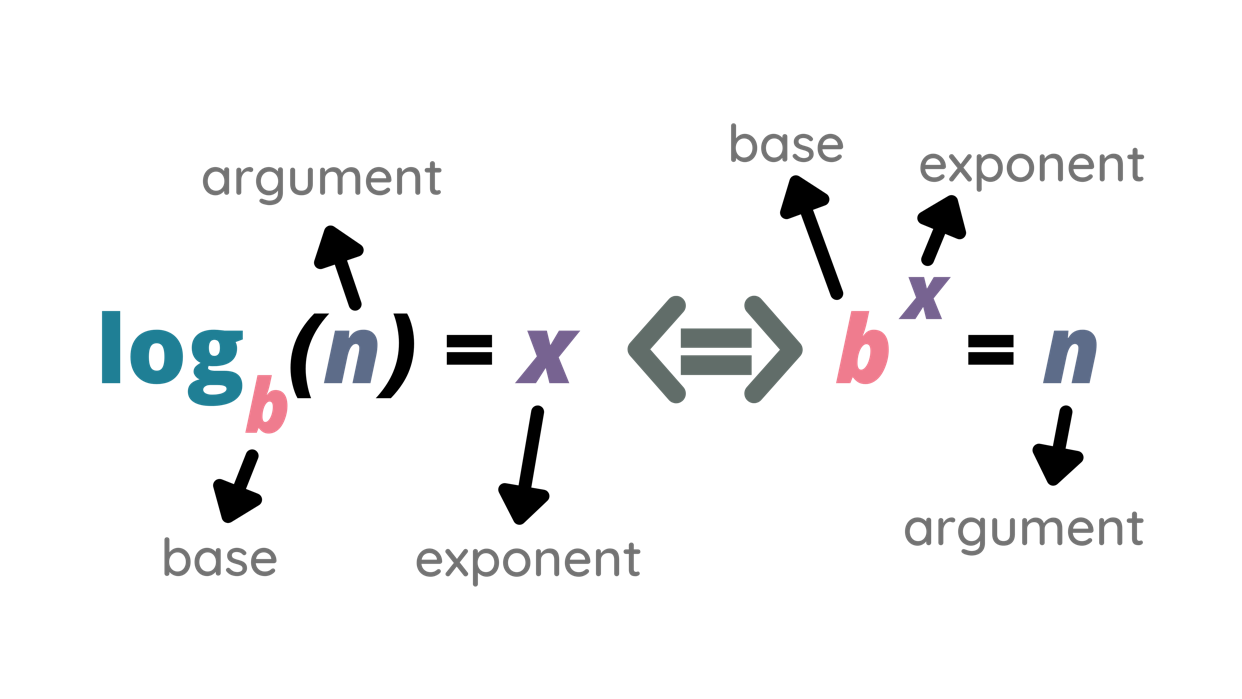
Applications

Logarithmic equations find applications across various fields, making equation calculators valuable tools in many areas:

• Physics & Chemistry: they are essential in calculating radioactive decay rates and determining acidity levels through the pH scale. In chemistry, the pH scale itself is logarithmic, defined as pH=−log⁡[H+], enabling chemists to handle a wide range of hydrogen ion concentrations efficiently.
• Finance & Economics: In finance, they help calculate compound interest and investment growth rates. Economists frequently use logarithms to analyze elasticity, facilitating the understanding of how variables such as price and quantity demanded interact. Logarithmic scales are also widely used in financial charts to represent percentage changes clearly, aiding traders and analysts in decision-making.
• Computer Science & Engineering: they play a critical role in algorithm complexity analysis. Algorithms with logarithmic time complexity, such as binary search, are highly efficient because their runtime grows slowly even as input size increases significantly. Engineers also utilize logarithms in signal processing tasks, including data compression and image enhancement techniques.
• Biology & Medicine: Biologists use this equations to model population growth and analyze drug concentration decay over time. Medical researchers apply logarithms to interpret biological data that spans multiple orders of magnitude, making complex biological relationships more manageable.
• Environmental Science & Geology: The Richter scale for measuring earthquake magnitudes is logarithmic, allowing geologists to quantify seismic activity effectively. Similarly, environmental scientists employ logarithmic functions to model phenomena like population dynamics or pollutant dispersion.
• Acoustics & Sound Engineering: The decibel scale used in acoustics is logarithmic, enabling sound engineers to measure sound intensity levels accurately. This scale compresses a vast range of sound volumes into a manageable numeric range, simplifying audio analysis and equipment calibration.
• Astronomy: Astronomers rely on logarithmic scales to measure stellar brightness (magnitude) and cosmic distances. These scales allow astronomers to represent enormous distances and brightness variations compactly and understandably.

Interestingly, even outside traditional scientific applications, logarithmic concepts subtly appear in everyday digital entertainment. For instance, understanding probability distributions in games like the popular coin master slot can involve logarithmic calculations indirectly when analyzing odds and payout structures.

The versatility of equations in these diverse fields underscores the importance of efficient tools like logarithmic equation calculators in modern scientific and professional work.

How to Use the Calculator

Using a logarithmic equation calculator is typically a straightforward process. Here’s a general guide:

1. Input the Equation: Enter your equation into the provided input field. Make sure to use the correct syntax as specified by the calculator.
2. Specify the Base: If your equation uses a base other than the common logarithm (base 10) or natural logarithm (base e), make sure to specify the base.
3. Select the Variable to Solve For: If your equation has multiple variables, specify which one you want to solve for.
4. Click Calculate: Once you’ve input all the necessary information, click the “Calculate” or “Solve” button.
5. Review the Results: The calculator will display the solution. Many calculators also provide step-by-step explanations of how the solution was reached.
6. Verify Your Answer: It’s always a good practice to verify the solution by plugging it back into the original equation.

Remember, while calculators are powerful tools, understanding the underlying concepts of logarithms is crucial for effective problem-solving and interpretation of results.

Features of the Logarithmic Equation Calculator

Modern logarithmic equation calculators come packed with features designed to simplify the problem-solving process. Here are some key features you can expect:

1. Multiple Base Options: These calculators support various bases, including common bases like 10 (common logarithm), e (natural logarithm), and 2, as well as custom bases.
2. Step-by-Step Solutions: Many calculators provide detailed, step-by-step solutions, helping users understand the problem-solving process.
3. User-Friendly Interface: Designed for ease of use, these calculators typically feature intuitive interfaces that make inputting equations straightforward.
4. Instant Results: Once an equation is input, these calculators provide immediate results, saving valuable time.
5. Versatility: Advanced calculators can handle a wide range of equations, from simple to complex.
6. Graphing Capabilities: Some calculators offer graphing functions, allowing users to visualize equations.
7. Equation Solving: Many calculators can solve for unknown variables in equations.
8. Additional Mathematical Functions: Besides logarithms, these calculators often include other mathematical functions, making them versatile tools for various calculations.

Examples

To better illustrate how a logarithmic equation calculator works, let’s explore two practical examples. These examples demonstrate clearly the calculator’s ability to solve logarithmic equations quickly and accurately, saving valuable time and minimizing errors that often occur during manual calculations.

These examples demonstrate how quickly and efficiently equation calculators can solve problems that would be time-consuming to compute manually.

Advantages of Using the Calculator

Logarithmic equation calculators offer numerous benefits that make them indispensable tools for students, educators, and professionals alike:

1. Accuracy: These calculators significantly reduce the risk of human error, ensuring precise results even for complex equations.
2. Time Efficiency: They provide instant solutions, saving considerable time compared to manual calculations. This is particularly beneficial when dealing with multiple or complex equations.
3. Educational Value: By providing step-by-step solutions, these calculators serve as excellent learning tools, helping users understand the problem-solving process.
4. Accessibility: Calculator is available online or as a mobile app, making it accessible anytime and anywhere.
5. Versatility: Advanced calculators can handle a wide range of logarithmic equations and often include additional mathematical functions.
6. Visualization: Some calculators offer graphing capabilities, allowing users to visualize logarithmic functions and better understand their behavior.
7. Consistency: These calculators provide a consistent approach to solving equations, eliminating variations that might occur with manual methods.
8. Confidence Building: For students and professionals alike, the ability to quickly verify solutions can boost confidence in mathematical problem-solving.

Comparison with Manual Methods

While manual methods of solving logarithmic equations have their place, particularly in building fundamental understanding, this equation calculators offer significant advantages:

Aspect	Manual Methods	Calculator Method
Time Consumption	High (minutes to hours)	Instantaneous results
Accuracy	Prone to errors	Highly accurate results
Complexity Handling	Difficult with complex equations	Handles complexity effortlessly
Learning Curve	Requires thorough understanding	Minimal learning curve
Availability	Limited by user’s skill level	Widely available online/apps
Consistency	May vary based on individual approach	Consistent results
Visualization	Limited to manual graphing	Often includes graphing capabilities

This comparison clearly illustrates the efficiency and reliability of using a logarithmic equation calculator, especially when dealing with complex or numerous equations.

Conclusion

Logarithmic equation calculators have revolutionized the way we approach and solve logarithmic problems. By offering speed, accuracy, and convenience, these tools have become indispensable in various fields, from academic studies to professional applications. They not only save time and reduce errors but also serve as valuable learning aids, helping users understand the intricacies of logarithmic equations.

As we continue to rely more on technology in our mathematical endeavors, logarithmic equation calculators stand out as prime examples of how digital tools can enhance our problem-solving capabilities. Whether you’re a student grappling with logarithmic concepts, a professional using them in complex models, or a researcher pushing the boundaries of scientific understanding, these calculators offer a powerful ally in your mathematical journey.

Embracing these tools while maintaining a solid understanding of the underlying principles of logarithms will undoubtedly lead to more efficient and accurate mathematical work across all disciplines.

FAQ