System of Linear Equations Calculator

A System of Linear Equations Calculator is an essential tool for anyone working with linear equations, whether in academics, research, or professional fields. Linear equations are foundational in mathematics and are widely used in various disciplines, including physics, engineering, economics, computer science, and data analysis. Solving these systems manually can be time-consuming and prone to errors, especially when dealing with multiple variables or complex coefficients. This is where a calculator becomes invaluable—it automates the process, ensuring accuracy while saving time.

This calculator is designed to handle a wide range of problems, from simple two-variable systems to more advanced multi-variable equations. It eliminates the need for tedious manual calculations by leveraging sophisticated algorithms that deliver precise solutions in seconds. Whether you’re solving equations for a school assignment or analyzing data for a real-world application, this tool provides clarity and efficiency.

What is a System of Linear Equations?

A system of linear equations is a fundamental concept in algebra and mathematics, forming the basis for solving problems that involve multiple variables and constraints. These systems consist of two or more linear equations that share the same set of variables, such as x, y, or z. Each equation represents a straight line (or a hyperplane in higher dimensions) when plotted on a graph. The goal of solving a system of linear equations is to determine the values of the variables that satisfy all the equations simultaneously.

For example, consider the system:

2x+y=5 and x−y=1

Here, x and y are the variables. Solving this system means finding the specific values of x and y that make both equations true at the same time. Graphically, this corresponds to finding the point where the two lines represented by these intersect. In this case, the solution is x=2 and y=1, which is the point of intersection.

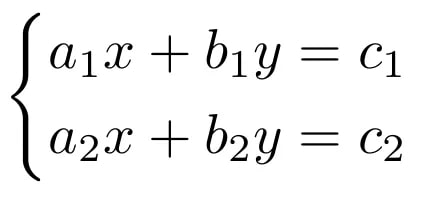
Features of the Calculator

The System of Linear Equations Calculator offers a range of features that make solving equations straightforward:

• Supports Multiple Variables: Solve systems with two, three, or more variables.
• Choice of Solving Methods: Includes substitution, elimination, matrix methods, and graphical solutions.
• User-Friendly Interface: Easy input fields for parameters.
• Error Detection: Identifies inconsistencies or errors in input equations.

How to Use the Calculator

Using a System of Linear Equations Calculator is designed to be a straightforward and user-friendly process, even for those new to solving equations. By following a few simple steps, you can quickly find solutions to your system, whether you’re working on a math problem, a physics application, or an engineering calculation. Below is a detailed guide to help you navigate the process effectively.

Input the Equations

The first step in using the calculator is entering your equations into the designated input fields. Here’s how to do it properly:

1. Ensure Consistency Across Variables: Make sure all equations use the same variables (e.g., x, y, z). Avoid mixing variable names like x and a unless they are part of your system.
2. Double-Check for Typos or Missing Coefficients: Verify that all coefficients and constants are entered correctly. For example, if an equation is x+y=5 but you accidentally type x+=5 or forget the coefficient for y, the calculator may produce errors or incorrect results.
3. Use Standard Mathematical Symbols: Use symbols like “+” for addition, “-” for subtraction, “=” for equality, and numerical coefficients as required. Avoid ambiguous notations or shorthand that could confuse the calculator.

View the Results

After selecting your solving method, click on the “Solve” or “Calculate” button to generate results. The calculator will process your input and provide the following outputs:

1. Solutions for Variables: The calculator will display the values of all variables that satisfy your system (e.g., x=2,y=1). If no solution exists (e.g., inconsistent system), it will indicate this clearly.
2. Step-by-Step Explanation (Optional): Many calculators offer detailed step-by-step solutions showing how each result was derived. This feature is especially helpful for students learning algebra or users who want to understand the methodology behind the solution.
3. Warnings or Error Messages: If there’s an issue with your input , the calculator will display an error message explaining what went wrong and how to fix it.

Tips for Best Results

To ensure accurate results and avoid common mistakes while using the calculator, keep these tips in mind:

• Double-Check Your Input: Even a small typo can lead to incorrect solutions or errors.
• Understand Your System Type: Knowing whether your system is consistent, inconsistent, or dependent can help you interpret results more effectively.
• Experiment with Different Methods: If time permits, try solving your system using multiple methods (e.g., substitution vs elimination) to compare results.
• Use Graphs for Verification: For two-variable systems, graphical representations can help confirm solutions visually.

By following these steps and tips, you’ll be able to leverage the full potential of a calculator and solve even complex problems with ease!

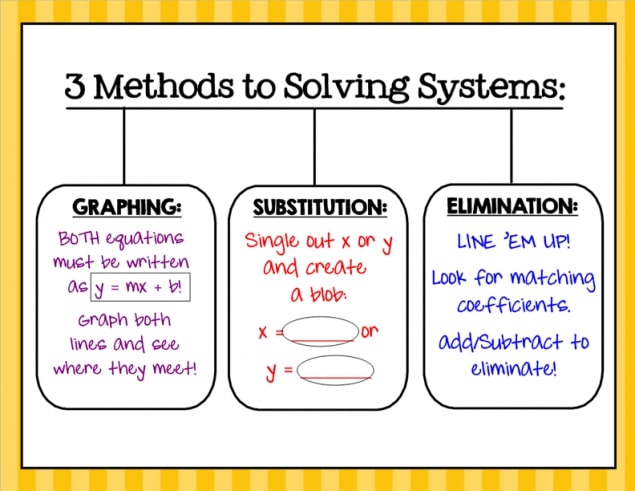
Solving Methods Explained

A System of Linear Equations Calculator is designed to accommodate various solving methods, each suited to different types of systems and user preferences. Understanding these methods can help you choose the most efficient approach for your problem. Below is a detailed explanation of the most commonly used solving methods supported by the calculator:

Substitution Method

The substitution method is one of the simplest and most intuitive ways to solve a system. It involves solving one equation for one variable and substituting that expression into the other equations. This method is particularly effective for systems with two variables but can also be applied to larger systems.

Steps to Solve Using Substitution:

1. Solve One Equation for One Variable: Choose one of the equations and isolate one variable in terms of the other(s). For example, from the equation x−y=1, solve for x: x=y+1
2. Substitute into the Other Equation(s): Replace the isolated variable in the remaining equation(s) with its expression. For example, substitute x=y+1 into 2x+y=5: 2(y+1)+y=5
3. Simplify and Solve for Remaining Variables: Simplify the resulting equation and solve for the remaining variable(s). In this case: 2y+2+y=5⟹3y=3⟹y=1
4. Back-Substitute to Find Other Variables: Use the value of y to find x by substituting it back into the expression x=y+1: x=1+1⟹x=2

Elimination Method

The elimination method involves adding or subtracting equations to eliminate one variable, making it easier to solve for the remaining variables. This method is especially useful when coefficients are aligned or can be easily manipulated to cancel out a variable.

Steps to Solve Using Elimination:

1. Align Equations: Write all equations in standard form (e.g., Ax+By=C) and align them vertically based on their variables. For example: 2x+y=5 x−y=1
2. Eliminate One Variable: Add or subtract the equations to cancel out one variable. In this case, add both equations to eliminate y: (2x+у)+(x−у)=5+1. Simplify: 3x=6⟹x=2
3. Substitute Back to Solve for Remaining Variables: Substitute x=2 into one of the original equations to solve for y: x−у=1⟹2−у=1⟹у=1; x=2, у=1

Matrix Method

The matrix method is a more advanced technique that uses linear algebra concepts like matrices and determinants to solve systems. This method is particularly powerful for larger systems with three or more variables but can also be applied to smaller systems.

Types of Systems of Linear Equations

Systems of linear equations can be classified into three main types:

Type	Description	Example
Consistent & Independent	Has exactly one unique solution (lines intersect at one point).	x+y=5, x−y=1
Consistent & Dependent	Has infinitely many solutions (lines overlap entirely).	2x+2y=10, x+y=5
Inconsistent	Has no solution (lines are parallel and never intersect).	x+y=5, x+y=7

Understanding these types helps in interpreting results from the calculator.

Common Errors and Troubleshooting

While using a calculator, you may encounter some common issues:

1. Input Errors:
   • Ensure coefficients are entered correctly.
   • Avoid leaving any variable undefined.
2. Inconsistent Systems:
   • The calculator may indicate “No Solution” if the system is inconsistent.
3. Dependent Systems:
   • For infinitely many solutions, expect results in parametric form.

Conclusion

The System of Linear Equations Calculator is an indispensable tool for solving systems quickly and accurately. With its wide range of features and solving methods, it caters to students and professionals alike. By understanding how to use it effectively and interpreting its results correctly, you can tackle even complex systems with ease.

FAQ