Understanding Quadratic Equations

Quadratic equations are among the cornerstones of modern mathematics, forming the basis for understanding curves, optimization, and motion. They appear in algebra, geometry, physics, and even machine learning. The general form of a quadratic equation is: ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0

where a, b, and c are real numbers, and a ≠ 0. The shape of the graph of a quadratic equation is a parabola, which can open upwards or downwards depending on the sign of a. This parabolic curve represents how variables change with acceleration or optimization — whether that’s the height of a thrown object, the profit of a business, or the brightness of a light beam.

Understanding how to manipulate this equation is essential for anyone studying mathematics, physics, or engineering, because it helps predict outcomes and optimize systems.

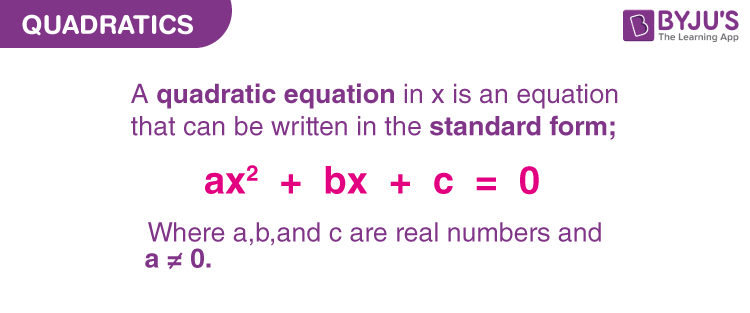
The Quadratic Formula

The most efficient way to solve a quadratic equation is by using the quadratic formula: x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}x=2a−b±b2−4ac​​

This universal formula works for all quadratic equations and provides exact solutions known as roots. The discriminant (D = b² – 4ac) reveals the nature of these roots, guiding you to understand whether the parabola intersects the x-axis, touches it at a single point, or floats above/below it without crossing.

Discriminant	Type of Roots	Graph Behavior	Example Equation
D > 0	Two distinct real roots	Parabola crosses x-axis twice	x² – 5x + 6 = 0
D = 0	One real repeated root	Parabola touches x-axis once	x² – 4x + 4 = 0
D < 0	Two complex roots	Parabola doesn’t cross x-axis	x² + 4x + 8 = 0

The discriminant is not only a numeric shortcut — it’s a window into the geometry of the equation. By analyzing D, mathematicians can instantly understand the behavior of an entire class of functions.

How to Use a Quadratic Equation Calculator

A quadratic equation calculator simplifies complex algebraic manipulation into a few quick steps. Instead of calculating manually, you can instantly obtain results and visualize how the parabola behaves.

To use the tool:

1. Enter the coefficients a, b, and c.
2. Click Calculate.
3. Instantly receive the discriminant, both roots, and an optional graph that plots the function.

Results:

These calculators are designed for students, educators, and engineers who want accuracy and efficiency. They save time and help prevent common algebraic errors. For example, in engineering or construction, using a calculator can verify the curvature of a structure or the stress points in a bridge design.

In educational settings, online tools allow learners to focus on concepts rather than computation, strengthening analytical thinking instead of repetitive arithmetic.

Mathematical Connections: Probability and Distributions

Mathematics is a beautifully interconnected discipline, where algebra, geometry, and probability often overlap. Just as quadratic equations model acceleration and optimization, probability distributions describe the likelihood of outcomes in random events. These mathematical patterns often reflect deep symmetry and balance, which can be visualized in games, physics, and natural systems.

Example: The Plinko App

In the Plinko App, a perfect illustration of probability in action, a small chip falls through a series of pegs, randomly bouncing left or right. With the simplifying assumption that each time a chip hits a peg there’s a 50% chance it goes left and a 50% chance it goes right, the distribution of outcomes follows the binomial distribution.

If we number the n slots from left to right, 0 to n–1, the probability of the chip landing in slot k is: P(k)=(n−1)!k!(n−1−k)!2n−1P(k) = \frac{(n-1)!}{k!(n-1-k)!2^{n-1}}P(k)=k!(n−1−k)!2n−1(n−1)!​

This mirrors the probability of flipping n–1 coins and getting k heads. It’s a fascinating link between combinatorics and randomness. Furthermore, as n increases indefinitely, the binomial distribution approaches the normal distribution, forming the familiar bell curve.

This same principle of mathematical balance is also found in quadratic equations — both reveal how symmetry emerges in nature and logic. In fact, just like the parabolic path of a projectile, the Plinko App visually demonstrates how repeated random choices produce a predictable and elegant pattern, beautifully illustrating the harmony between algebra and probability.

Applications of Quadratic Equations

Quadratic equations appear across virtually all fields of science and technology. They model motion, energy, growth, and optimization — making them indispensable tools for analysis and prediction.

• Physics: used to describe trajectories, motion under gravity, and energy conservation.
• Engineering: determines the design of parabolic antennas, arches, and suspension systems.
• Economics: models profit maximization, cost minimization, and equilibrium points.
• Computer Graphics: creates smooth curved surfaces and visual effects in games and animations.
• Data Science: helps fit curves to data for trend prediction and analysis.

Field	Real-World Application	Quadratic Role
Physics	Projectile motion	Describes acceleration and trajectory
Architecture	Parabolic bridge arches	Ensures optimal load distribution
Economics	Profit and cost optimization	Determines maximum or minimum values
Machine Learning	Curve fitting and regression	Models relationships in datasets

By mastering quadratic equations, you gain a mathematical key to solving practical problems in countless domains. From a falling object’s height to the curved path of light — quadratics describe how the world behaves.

Summary

Quadratic equations are more than just abstract formulas — they are the mathematical framework for understanding motion, balance, and natural symmetry. Whether calculating roots, exploring curves, or analyzing probability in the Plinko App, the principles remain universal.

The beauty of mathematics lies in its consistency: quadratic equations reveal structure, while probability uncovers randomness. Together, they demonstrate that even in uncertainty, patterns emerge — precise, predictable, and profoundly elegant.

FAQ